Komplex természettudományi verseny
Második forduló
2. Fizika (kapcsolások) (letöltés pdf-ben)
2.1. Eredő rugóállandó kiszámítása
a) Az ábrán látható expanderbe 5 darab egyforma, 40 N/m rugóállandójú, 60 centiméteres rugót teszünk. Mekkora erővel lehet 150 centiméterre kinyújtani a sporteszközt?

b) Azonos hosszúságú, de különböző rugóállandójú rugókat párhuzamosan összekapcsolunk (mint az expanderben). A Newton-törvények segítségével igazoljuk, hogy a rugókat helyettesítő egyetlen rugó „eredő” rugóállandója:
![]()
b) Azonos hosszúságú, de különböző rugóállandójú rugókat egymás után sorban összekapcsolunk. A Newton-törvények segítségével igazoljuk, hogy
![]()
2.2. Eredő kapacitás kiszámítása
Egy elhanyagolható ellenállású drótból készült kocka minden élének közepén egy–egy 12 pikofarád kapacitású kondenzátor található az ábrán látható módon. Az A pontban az elektromos potenciál értéke UA=24 V; a B pontban a potenciál értéke zérus.
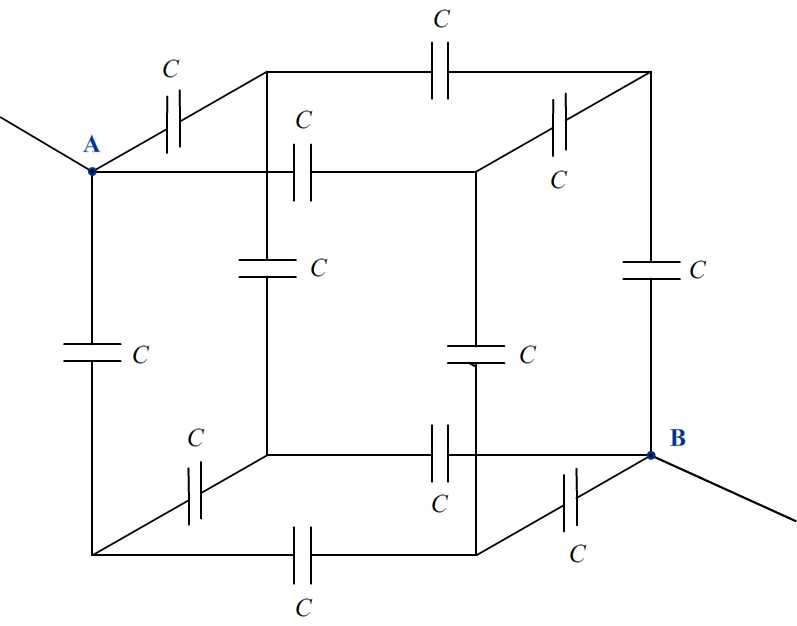
- Határozzuk meg az eredő kapacitást!
- Mekkora töltés jut az egyes kondenzátorokra?
- Határozzuk meg a kocka csúcsaiban az elektromos potenciált!
2.3. Eredő ellenállás kiszámítása
Egy elhanyagolható ellenállású drótból készült kocka minden élének közepén egy–egy 12 ohmos ellenállás található az ábrán látható módon. Az A pontban az elektromos potenciál értéke UA=24 V; a B pontban a potenciál értéke zérus.
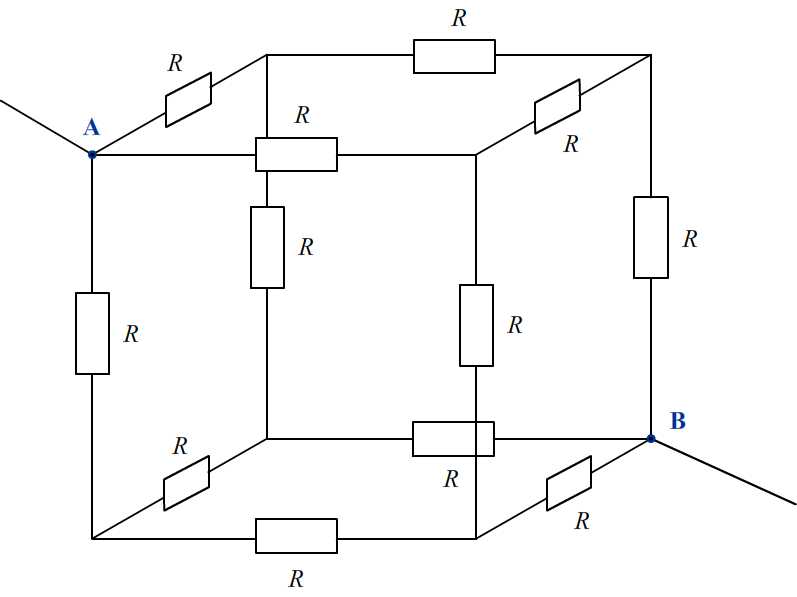
- Határozzuk meg az eredő ellenállást!
- Mekkora az áramerősség az egyes ágakban?
- Határozzuk meg a kocka csúcsaiban az elektromos potenciált!
